Meta Matrix Library
Home About FAQ Install Documentation To Do Download Related Links

Tutorial   Modules   Alphabetical List   Data Structures   File List   Data Fields   Globals   Related Pages (e.g. ToDo)  
src

itsl.c File Reference

Implementation of the iterative solvers like gmres, minres. More...

#include "itsl.h"

Functions

ME_MATRIX * itsl_jacobi_preconditioner (ME_MATRIX *M)
 Jacobi Preconditioner 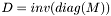$ D = inv (diag(M)) $.
int itsl_minres (const ME_MATRIX *A, const VECTOR *b, VECTOR *guess, const MEML_FLOAT eps)
int itsl_arnoldi (const ME_MATRIX *A, VECTOR *r, ME_MATRIX **H, ME_MATRIX **Q, MEML_INT const krylow_dim)
int itsl_least_square_solve_f (const ME_MATRIX *M, const VECTOR *b, VECTOR *result)
void itsl_gmres (const ME_MATRIX *A, const VECTOR *b, VECTOR *guess, const MEML_FLOAT boundary, const int krylov_dim)
 grmes without precondioner
void itsl_gmres_jacobi (const ME_MATRIX *M, const VECTOR *f, VECTOR *guess, const MEML_FLOAT boundary, const int krylov_dim)
 grmes with jacobi precondioner

Detailed Description

Implementation of the iterative solvers like gmres, minres.

Author:
Joerg Frochte

Function Documentation

int itsl_arnoldi (  const ME_MATRIX *  A,
VECTOR *  r,
ME_MATRIX **  H,
ME_MATRIX **  Q,
MEML_INT const   krylow_dim
) 
 

The Arnoldi iteration for computing a Krylov subspace of the dimension krylow_dim

void itsl_gmres (  const ME_MATRIX *  A,
const VECTOR *  b,
VECTOR *  guess,
const MEML_FLOAT  boundary,
const int  krylov_dim
) 
 

grmes without precondioner

This function solves the linear equation system Ax=b, based on the grmes-algorithm.

Parameters:
A a matrix
b a vector; the right side for the linear equation system
guess is a initial guess of the result x. If you don't have one,set guess to the zero-vector. In the end guess stores the result.
krylov_dim the dimension of the krylov-space created by the itsl_sf_arnoldi function. A small dimension will bring a loos of speed, a greater k will requiere more memory. 25-100 is a mostly a good choise for k.
boundary itsl_gmres breaks if $ \|A*guess -b \| < boundary v $

void itsl_gmres_jacobi (  const ME_MATRIX *  M,
const VECTOR *  f,
VECTOR *  guess,
const MEML_FLOAT  boundary,
const int  krylov_dim
) 
 

grmes with jacobi precondioner

This function solves the linear equation system Ax=b, based on the grmes-algorithm.

Parameters:
A a matrix
b a vector; the right side for the linear equation system
guess is a initial guess of the result x. If you don't have one,set guess to the zero-vector. In the end guess stores the result.
krylov_dim the dimension of the krylov-space created by the itsl_sf_arnoldi function. A small dimension will bring a loos of speed, a greater k will requiere more memory. 25-100 is a mostly a good choise for k.
boundary itsl_gmres breaks if $ \|A*guess -b \| < boundary v $

ME_MATRIX* itsl_jacobi_preconditioner (  ME_MATRIX *  M  ) 
 

Jacobi Preconditioner $ D = inv (diag(M)) $.

int itsl_least_square_solve_f (  const ME_MATRIX *  M,
const VECTOR *  b,
VECTOR *  result
) 
 

Computes the solution of a balance problem

$ M \in R^{n \times k} \; ; \; b \in R^n $
$ \min_{x\in R^k} \|b-M*x\| $.

int itsl_minres (  const ME_MATRIX *  A,
const VECTOR *  b,
VECTOR *  guess,
const MEML_FLOAT  eps
) 
 

Generated on Tue Mar 28 14:10:38 2006 by  doxygen 1.4.1