|
Functions |
| ME_MATRIX * | meml_matrix_scaling (const MEML_FLOAT alpha, const ME_MATRIX *M) |
| | 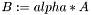
|
| void | meml_matrix_scaling_f (const MEML_FLOAT alpha, ME_MATRIX *M) |
| | 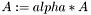
|
| MEML_FLOAT | meml_matrix_norm (const ME_MATRIX *M) |
| | 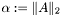
|
| MEML_FLOAT | meml_matrix_norm_inf (const ME_MATRIX *M) |
| | 
|
| MEML_FLOAT | meml_matrix_norm_1 (const ME_MATRIX *M) |
| | 
|
| MEML_FLOAT | meml_matrix_norm_frobenius (const ME_MATRIX *M) |
| | 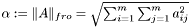
|
| void | meml_matrix_rank_one_update_f (const MEML_FLOAT alpha, const VECTOR *x, const VECTOR *y, ME_MATRIX *M) |
| | 
|
| ME_MATRIX * | meml_matrix_rank_one_update (const MEML_FLOAT alpha, const VECTOR *x, const VECTOR *y, const ME_MATRIX *M) |
| | 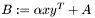
|
| ME_MATRIX * | meml_matrix_mul (const ME_MATRIX *A, const ME_MATRIX *B) |
| | 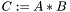
|
| void | meml_matrix_mul_f (const ME_MATRIX *A, const ME_MATRIX *B, ME_MATRIX **C) |
| | 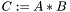
|
| void | meml_matrix_mul_ff (const MEML_FLOAT alpha, const ME_MATRIX *A, const ME_MATRIX *B, const MEML_FLOAT beta, ME_MATRIX **C) |
| | 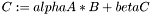
|
| ME_MATRIX * | meml_matrix_add (const ME_MATRIX *A, const ME_MATRIX *B) |
| | 
|
| void | meml_matrix_add_f (const ME_MATRIX *A, ME_MATRIX *B) |
| | 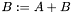
|
| ME_MATRIX * | meml_matrix_trans (ME_MATRIX *M) |
| | A : = M'.
|
| void | meml_matrix_trans_f (ME_MATRIX **M) |
| | M : = M'.
|
| int | meml_matrix_qr (const ME_MATRIX *M, ME_MATRIX **Q, ME_MATRIX **R) |
| | QR = M.
|
| ME_MATRIX * | meml_matrix_eig_f (const ME_MATRIX *M, VECTOR *wr, VECTOR *wi) |
| void | meml_matrix_eig (const ME_MATRIX *M, VECTOR *wr, VECTOR *wi) |
| VECTOR * | meml_matrix_svd (const ME_MATRIX *A) |
| int | meml_matrix_svd_f (const ME_MATRIX *A, VECTOR *s) |
| MEML_INT | meml_matrix_rank (const ME_MATRIX *M) |
| | rank of a matrix
|
| ME_MATRIX * | meml_matrix_lu (const ME_MATRIX *M, ME_MATRIX *L, ME_MATRIX *U) |
| | M = P * L * U.
|
| int | meml_matrix_equal (const ME_MATRIX *A, const ME_MATRIX *B) |
| | returns 1 if A=B and 0 if A  B B
|


 1.4.1
1.4.1